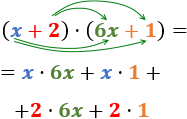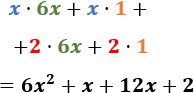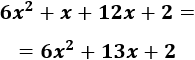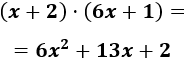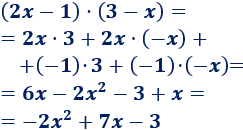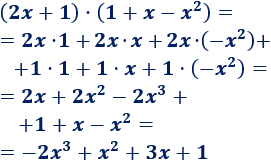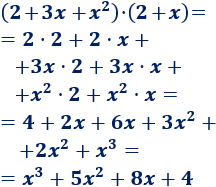31 de Octubre 2020
- Ver videos adjuntos donde se explica el área temática (Vía WhatsApp)
- Ver videos adjuntos donde se explica el área temática http://www.stllna.com/w0
- Actividad
17 de Octubre 2020
03 de Octubre 2020
- Explicación actividad y desarrollo taller de matemática financiera
26 de septiembre 2020
- Ver videos adjuntos donde se explica el área temática (Vía WhatsApp)
- Actividad
22 De Agosto 2020
Multiplicación entre polinomios
Ejemplo 2
Vamos a multiplicar los binomios x+2 y 6x+1.
Primero, multiplicamos el monomio x del primer polinomio por los dos monomios del segundo. Después, hacemos lo mismo con el segundo monomio (+2):
Simplificamos el resultado (multiplicando los coeficientes y sumando los exponentes de las partes literales):
Podemos simplificar más:
Por tanto,
Ejemplo 3
Hay que tener cuidado con los signos negativos: debemos aplicar la regla de los signos.
Ejemplo 4
Tenemos que multiplicar un binomio por un trinomio:
Ejemplo 5
Tenemos que multiplicar un trinomio por un binomio:
Ver el siguiente enlace con la explicación para ampliar el tema:
Actividad
8 De Agosto 2020
Adición y sustracción de polinomios
Ver el video: https://youtu.be/Pj95vjGSctg
Video del docente via whatsap
Multiplicación entre polinomios
18 De julio 2020


Actividad
FECHA: 10/06/2020
La siguiente actividad se debe realizar fuera de la institución para ello se recomienda tener en cuenta las siguientes recomendaciones:
1. Leer detenidamente la actividad completa.
2. Empezar a desarrollar la temática en el horario de clase.
3. Ser puntuales para no perderse la actividad de iniciación.
4. La guía no es necesaria transcribirla al cuaderno, los que deseen la pueden imprimir para tenerla como material de estudio.
ACTIVIDAD N° 8
TEMA: Números racionales en la recta numérica y orden de fracciones
OBJETIVO:
Ubicar números fraccionarios en la recta numérica
Comparar fracciones en cualquier contexto.
ACTIVIDAD INICIAL:
Observar el siguiente vídeo introductorio sobre racionales.
Observar el siguiente vídeo introductorio sobre racionales.
MARCO TEÓRICO:
Números racionales en la recta numérica
Para representar el peso de cada costal en la recta numérica, primero se debe
expresar cada peso en fracciones con el mismo denominador.
Posteriormente, se divide cada unidad de la recta según lo que indica el
denominador (ocho partes iguales) y se toman tantas partes como indique el
numerador. La representación de los pesos en la recta numérica se observa en la
Figura
Los números racionales se ubican en la recta numérica tanto a la izquierda como
a la derecha del 0. A la derecha se hallan los racionales positivos y a la izquierda los
racionales negativos.
Ten en cuenta
Al representar un número racional
dado (en su forma fraccionaria) en
la recta numérica, cada unidad debe
dividirse en tantas partes iguales como
indique el denominador.
Ejemplo
Si se divide en dos partes iguales cada segmento unidad en la recta numérica,
podemos representar los números racionales cuya representación fraccionaria
tenga como denominador 2. En la recta numérica de la Figura se observa la
representación de los números racionales 3 /2 , 7 /2 , - 1 /2 y - 5 /2 .
Relación de orden en los números racionales:
El profesor Camilo preguntó a sus
32 estudiantes acerca de su deporte
favorito y anotó la fracción de los
que eligieron cada deporte en la
Tabla
¿Cuál es el orden de popularidad
de los deportes?
Para responder la pregunta, se puede construir una recta numérica como la de
la Figura 1 y ubicar en ella cada fracción. El orden de mayor a menor preferencia
corresponde a las fracciones ubicadas de derecha a izquierda.
De acuerdo con el criterio indicado, el orden de los deportes desde el de mayor
aceptación al menos popular es: primero natación, luego tenis y fútbol (con el mismo
grado de aceptación), y por último, béisbol.
Para comparar dos números racionales, se deben tener en cuenta varios criterios:
• Todo número racional positivo es mayor que cualquier racional negativo.
• Todo número racional negativo es menor que 0.
• Si dos números racionales positivos tienen igual denominador, es menor el que
tiene menor numerador.
Por ejemplo:
• Si dos números racionales positivos tienen el mismo numerador, es menor el
que tiene mayor denominador.
Por ejemplo.
- Si dos números racionales tienen distinto denominador, se debe buscar una fracción equivalente a cada una de las fracciones dadas, con el mismo denominador, y compararlas teniendo en cuenta los criterios anteriores.
Ejemplo:
Para comparar los números racionales 3/10 y 1/9 se pueden seguir estos pasos:
• Se encuentra el mínimo común múltiplo de los denominadores; esto es, 90.
• Se amplifican las fracciones para expresarlas con denominador 90.
ACTIVIDADES PRACTICAS:
2. En una competencia de patinaje, los tres competidores que se disputaban
el paso a la final registraron los siguientes tiempos: Juan 3/4 de hora, Camilo
1/2 de hora y Fernando 8/15 de hora. ¿Cuál de los tres llegó en primer lugar?
3. Ordena de menor a mayor los números racionales de
cada lista.
4. Representa en la recta numérica cada número racional.
TRABAJO EXTRA CLASE:
Resolver los siguientes ejercicios y enviar el trabajo por correo antes del próximo miércoles.
2. Para el diseño hidráulico de un edificio, el ingeniero
utilizará tubería de tres diámetros diferentes: tubería
tipo A, de media pulgada; tubería tipo B, de tres
octavos de pulgada, y tubería tipo C, de tres cuartos
de pulgada. ¿Cuál es el orden de menor a mayor de los
tres tipos de tubería, de acuerdo con la magnitud de
su diámetro?

FECHA: 28/05/2020
La siguiente actividad se debe realizar fuera de la institución para ello se recomienda tener en cuenta las siguientes recomendaciones:
1. Leer detenidamente la actividad completa.
2. Empezar a desarrollar la temática en el horario de clase.
3. Ser puntuales para no perderse la actividad de iniciación.
4. La guía no es necesaria transcribirla al cuaderno, los que deseen la pueden imprimir para tenerla como material de estudio.
La siguiente actividad se debe realizar fuera de la institución para ello se recomienda tener en cuenta las siguientes recomendaciones:
1. Leer detenidamente la actividad completa.
2. Empezar a desarrollar la temática en el horario de clase.
3. Ser puntuales para no perderse la actividad de iniciación.
4. La guía no es necesaria transcribirla al cuaderno, los que deseen la pueden imprimir para tenerla como material de estudio.
ACTIVIDAD N° 7
TEMA: FRACCIONES EQUIVALENTES Y FRACCIONES IRREDUCIBLES
OBJETIVO: Reconocer cuando dos fracciones o mas son equivalentes, e identificar si una fracción es irreducible.
ACTIVIDAD INICIAL:
Observar el siguiente vídeo introductorio sobre racionales.
Observar el siguiente vídeo introductorio sobre racionales.
MARCO TEÓRICO:
EL CONJUNTO DE LOS NÚMEROS RACIONALES
Un número racional es el conjunto de todas las fracciones equivalentes a una dada. Se toma como representante de este número la fracción irreducible.
El conjunto de los números racionales (Q) está formado por los números de la forma a / b , en donde a y b son números enteros y b es diferente de 0.
Este conjunto contiene a los números enteros que, a su vez, contiene a los naturales, tal como se muestra en la Figura.
Para determinar el signo de un número racional, basta con observar los signos del numerador y del denominador: si son iguales, el racional es positivo; si no lo son, el racional es negativo.
Fracciones equivalentes
Se denominan fracciones equivalentes aquellas fracciones que representan la misma cantidad o parte del todo. En general, a / b = c / d si y solo si a * d = b * c.
Ejemplo:
Al simplificar la fracción 9 / 27 se obtiene 1 / 3 , que es equivalente a la primera
fracción. Es decir,
9 / 27 = 1 / 3
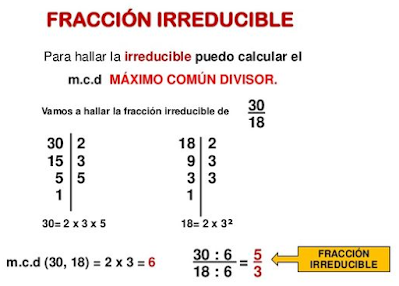
Fracciones irreducibles
Se denominan fracciones irreducibles aquellas fracciones en las que el máximo común divisor entre el numerador y el denominador es 1; o, de otra forma, aquellas que están simplificadas al máximo.
Ten en cuenta
• Para simplificar una fracción, se dividen tanto el numerador como el denominador por un divisor común a ambos.
• Cuando para simplificar se elige justo el máximo común divisor, la fracción que se obtiene es irreducible.
Observa el siguiente vídeo.
ACTIVIDADES PRACTICAS:
1. Escribe tres números racionales equivalentes a cada racional dado.
a. 2 / 5
b. - 1 / 7
c. 2 / 3
d. 9 / 5
e.- 3 / 2
2. Halla la fracción irreducible equivalente a cada número racional.
a. 24 / 48
b. -18 / 9
c. 16 / 48
d. 3 / 9
e. -12 /36
TRABAJO EXTRA CLASE:
Resolver los siguientes ejercicios y enviar el trabajo por correo antes del próximo miércoles.
2. Dos buses escolares transportan cada uno 24 estudiantes. En el primero, 1 / 4 de los pasajeros son niñas y en el segundo, 3 / 12 lo son.
• ¿Qué se puede afirmar con respecto a la cantidad de niñas que se transportan en cada bus?
3. Leonardo consume 12 / 4 de litro de agua a la semana.
¿Cuánta agua consume en un mes?
4. Un quinto de los 125 espectadores de una película salieron satisfechos.
¿Cuántos no salieron satisfechos?
5. En un hospital se atienden diariamente doce personas de la tercera edad por cada cuatro niños. ¿Cuántas personas de la tercera edad fueron atendidas en el mes, si durante ese tiempo se atendieron 120 niños?

FECHA: 13/05/2020
La siguiente actividad se debe realizar fuera de la institución para ello se recomienda tener en cuenta las siguientes recomendaciones:
1. Leer detenidamente la actividad completa.
2. Empezar a desarrollar la temática en el horario de clase.
3. Ser puntuales para no perderse la actividad de iniciación.
4. La guía no es necesaria transcribirla al cuaderno, los que deseen la pueden imprimir para tenerla como material de estudio.
La siguiente actividad se debe realizar fuera de la institución para ello se recomienda tener en cuenta las siguientes recomendaciones:
1. Leer detenidamente la actividad completa.
2. Empezar a desarrollar la temática en el horario de clase.
3. Ser puntuales para no perderse la actividad de iniciación.
4. La guía no es necesaria transcribirla al cuaderno, los que deseen la pueden imprimir para tenerla como material de estudio.
ACTIVIDAD N° 6
TEMA: m.c.m y M.C.D
OBJETIVO: Resolver situaciones de la vida cotidiana que requieran el uso del m.c.m y el M.C.D.
ACTIVIDAD INICIAL:
Observar el siguiente vídeo que les ayudara a comprender como trabajar la descomposición en factores primos.
Observar el siguiente vídeo que les ayudara a comprender como trabajar la descomposición en factores primos.
MARCO TEÓRICO:
El máximo común divisor (M.C.D)
El máximo común divisor (M.C.D) de dos o más números es el mayor número que divide exactamente a todos.
Cálculo del M.C.D
Se descomponen los números en factores primos.
Se toman los factores comunes del número que se repite más veces.
Se multiplican dichos factores y el resultado obtenido es el M.C.D.
El mínimo común múltiplo (m.c.m)
El mínimo común múltiplo (m.c.m) de dos o más números es el menor número que contiene exactamente a todos.
Cálculo del m.c.m
Se descomponen los números en factores primos.
Se toman los factores comunes y no comunes que ser repiten más veces.
Se multiplican dichos factores y el resultado obtenido es el m.c.m.
ACTIVIDADES PRACTICAS:
Los siguientes ejercicios son para realizar en clase y enviarlos por foto al finalizar.
1. Descomponer los siguientes números en factores primos y calcula su M.C.D.
a) 320 y 180
2. Descomponer los siguientes números en factores primos y calcular su m.c.m
a. 18, 27 y 30
3. Calculamos
el mcm y el MCD de 96, 240 y 180
TRABAJO EXTRA CLASE:
Resolver los siguientes ejercicios y enviar el trabajo por correo antes del próximo miércoles.
1. Un campesino llena 3 vasijas de leche, cuyas capacidades son: 24 litros, 36 litros y 54 litros. ¿Cuántos litros de capacidad deben tener las botellas para que en ellas se pueda envasar la misma cantidad de leche?
2. Tres series de luces de navidad se encienden de la siguiente manera: la primera serie cada 15 segundos, la segunda cada 20 segundos y la tercera cada minuto. Si las tres series de luces se encendieron simultáneamente a las 18h00, ¿a qué hora volverán a coincidir encendidas?
3. Roberto quiere cortar dos listones de madera en partes iguales para enrollarlos en plástico y guardarlos. Pero quiere cortarlos lo más largo posible para no desaprovecharlos. Si los listones miden 246cm y 328cm, ¿cuánto deben medir los trozos?
4. Jaime está practicando al béisbol con dos lanzadoras de bolas y su hermana Laura está anotando los resultados. Como de momento Jaime no ha fallado ningún tiro, Laura programa las lanzadoras para que una dispare cada 12 segundos y la otra, cada 16 segundos. ¿Cuánto tiempo tardarán las máquinas en lanzar una bola al mismo tiempo por primera vez?
5. Calculamos el mínimo común múltiplo y el maximo comun divisor de 180 y 324

FECHA: 29/04/2020
La siguiente actividad se debe realizar fuera de la institución para ello se recomienda tener en cuenta las siguientes recomendaciones:
1. Leer detenidamente la actividad completa.
2. Empezar a desarrollar la temática en el horario de clase.
3. Ser puntuales para no perderse la actividad de iniciación.
4. La guía no es necesaria transcribirla al cuaderno, los que deseen la pueden imprimir para tenerla como material de estudio.
ACTIVIDAD N° 5
TEMA: Múltiplos y Divisores.
OBJETIVO: Identificar múltiplos y divisores de un conjunto de números naturales.
ACTIVIDAD INICIAL:
Observar el siguiente vídeo que les ayudara a comprender y diferenciar un número primo de un número compuesto.
Observar el siguiente vídeo que les ayudara a comprender y diferenciar un número primo de un número compuesto.
MARCO TEÓRICO:
MÚLTIPLOS:
Un número es múltiplo de otro cuando le contiene un número exacto de veces.
Ejemplo:
El 15 es múltiplo de 5 porque le contiene 3 veces.
15 = 5 x 5 x 5
Propiedades:
- El cero es múltiplo de todos los números, por ejemplo:
- La suma de varios múltiplos de un número es otro múltiplo de dicho número, por ejemplo:
- La diferencia de dos múltiplos de un número es otro múltiplo de dicho número, por ejemplo:
- Si un número es múltiplo de otro, todos los múltiplos del primero lo son también del segundo, por ejemplo:
Para hallar los múltiplos de un número, basta con construir su tabla de multiplicar.
DIVISORES
Un número es divisor de otro si cuando dividimos el segundo entre el primero, el residuo de la división es 0.
En otras palabras: Decimos que un número a es divisor de otro número b, si la división de b entre a es exacta.
Propiedades de los divisores:
1. Todo número entero distinto de 0 es divisor de sí mismo, por ejemplo:
8 ÷ 8 = 1; 15 ÷ 15 = 1
2. El 1 es divisor de todos los números, por ejemplo:
54 ÷ 1 = 54; 36 ÷ 1 = 36
3. Si un número es divisor de otros dos, también lo es de su suma y de su diferencia, por ejemplo:
6 es D12 y D36, y 12 + 36 = 48, entonces 6 es D48;
por otro lado, 36 – 12 = 24 y 6 es D24.
4. Si un número es divisor de otro, también lo es de cualquier múltiplo de este, por ejemplo:
4 es D12 y los M12 son (12, 24, 36, 48, 60…)
5. Si un número es divisor de otro y este lo es de un tercero, el primero lo es del tercero, por ejemplo:
2 es D4; 4 es D16; entonces 2 es D16.
CRITERIOS DE DIVISIBILIDAD
Nos permiten saber de un modo sencillo cuando un número es divisible por otro.
ACTIVIDADES PRACTICAS:
Los siguientes ejercicios son para realizar en clase y enviarlos por foto al finalizar.
1. Halla cinco números que sean múltiplos de 5 y menores que 60.
2. Completa la serie de múltiplos de 3 hasta el 30. M(3)={0, 3, 6, 9, ...........}
3. Señala cuales de los siguientes números son múltiplos comunes de 5 y de 7.
35, 10, 70, 14, 700, 140, 20
4. Busca los seis divisores de 12.
5. Busca todos los divisores de 15.
6. Busca todos los divisores de 20.
TRABAJO EXTRA CLASE:
Resolver los siguientes ejercicios y enviar el trabajo por correo antes del próximo miércoles.
1. Calcula los números primos comprendidos entre el 1 y el 100
2. Calcula los divisores comunes de 12 y 20
3. Calcula los divisores comunes de 25 y 30
4. Calcula los divisores comunes de 12, 20 y 24.
5. Calcula los múltiplos comunes de 3 y 5 menores que 50.
6. Resuelve:
7. Resuelve

FECHA: 20/03/2020
La siguiente actividad se debe realizar fuera de la institución para ello se recomienda tener en cuenta las siguientes recomendaciones:
1. Leer detenidamente la actividad completa.
2. Empezar a desarrollar la temática en el horario de clase.
3. Ser puntuales para no perderse la actividad de iniciación.
4. La guía no es necesaria transcribirla al cuaderno, los que deseen la pueden imprimir para tenerla como material de estudio.
ACTIVIDAD N° 4
TEMA: Potencias y Raíces de números enteros (Z).
OBJETIVO: Resuelve situaciones de la vida cotidiana que involucren operaciones combinadas con números enteros, por medio de la practica y solución de ejercicios matemáticos.
ACTIVIDAD INICIAL:
Observar el siguiente vídeo que ayudara a recordar como trabajar las operaciones combinadas con números enteros.
MARCO TEÓRICO:
Potencias y Raíces con Números enteros (Z)
Potencias de base entera y exponente natural:
Una potencia es una forma abreviada de escribir una multiplicación de factores iguales. La base de la potencia es el factor que se repite. El exponente es el número de veces que se repite.
Observar el siguiente vídeo que ayudara a recordar como trabajar las operaciones combinadas con números enteros.
MARCO TEÓRICO:
Potencias y Raíces con Números enteros (Z)
Potencias de base entera y exponente natural:
Una potencia es una forma abreviada de escribir una multiplicación de factores iguales. La base de la potencia es el factor que se repite. El exponente es el número de veces que se repite.
Potencias de base un número entero negativo:
• Si la base es negativa y el exponente es par, el valor de la potencia es positivo.
• Si la base es negativa y el exponente es impar, el valor de la potencia es negativo.
Propiedades de las potencias:
El producto de potencias de la misma base es igual a otra potencia de la misma base y con el exponente igual a la suma de los exponentes de los factores.
En general, se cumple que:
El cociente de potencias de la misma base es igual a otra potencia de la misma base y con el exponente igual a la diferencia entre el exponente del dividendo y el exponente del divisor. En general, se cumple que:
La potencia de una potencia es igual a la misma base elevada al producto de los exponentes. En general, se cumple que:
El producto de potencias con el mismo exponente es una potencia con el mismo exponente y cuya base es el producto de las bases. En general, se cumple que:
El cociente de potencias con el mismo exponente es una potencia con el mismo exponente y cuya base es el cociente de las bases. En general, se cumple que:
Raíces cuadradas
La radiación es una operación inversa de la potenciación, con la cual se busca la base conociendo el exponente y la potencia.
La raíz cuadrada exacta de un número es otro número que multiplicado por sí mismo sea igual al primer número. Se expresa así:
Hallar la raíz de un número a significa encontrar un número b que, multiplicado por sí mismo, sea igual a a.
Ejemplos:
Jerarquía de las operaciones con potencias y raíces:
Para efectuar operaciones combinadas con potencias y raíces, se sigue este orden:
• Se efectúan las potencias y raíces.
• Se resuelven las operaciones que estén dentro de los signos de agrupación. Si hay varios, unos dentro de otros, se empieza por los internos.
• Se realizan las multiplicaciones y divisiones de izquierda a derecha.
• Se calculan las adiciones y sustracciones de izquierda a derecha.
DESARROLLO DE COMPETENCIAS:
1. Leer la información presentada del tema, ver los vídeos y tratar de entender los ejemplos. si surge alguna inquietud preguntar por el grupo en el horario establecido de clase.
ACTIVIDADES PRACTICAS:
Las siguientes actividades son para realizar en horario de clase, no se deben entregar son para practicar el tema y saber si surge alguna inquietud.
1. Resolver:
1) 2 – 5 * 7 =
2) –5 – (3 + 4 * –6) + 1 =
3) –4 + 6 * –2 – –8 * 7 =
4) –18 * 6 – (–7 * 6 +) –9 =
5) –12 – 24 + 6 * –5 =
6) 4 – 5 –(–6 – 7 * 8) + 9 =
a) 3√2 + 5√2 - 7√2 =
b) 5√5 + 4√20 - 3√45 =
c) 2 3√54 - 3√24 - 33√16 =
d) 3√2 + 2√3 - √12 =
TRABAJO EXTRA CLASE
FECHA: 06/03/2020
ACTIVIDAD N° 3
TEMA: Operaciones combinadas con números enteros (Z)
OBJETIVO: Resuelve situaciones de la vida cotidiana que involucren operaciones combinadas con números enteros, por medio de la practica y solución de ejercicios matemáticos.
ACTIVIDAD INICIAL:
Juegos de ingenio matemático que ayuden a desarrollar el pensamiento lógico y predispongan al grupo para la comprensión del nuevo tema.
MARCO TEÓRICO:
Para efectuar operaciones combinadas con números enteros, se sigue este orden:
1. Se resuelven las multiplicaciones y divisiones de izquierda a derecha.
2. Se resuelven las adiciones y sustracciones de izquierda a derecha.
Operaciones con paréntesis
Cuando hay operaciones combinadas en las que aparecen signos de agrupación, el orden para resolverlas es el siguiente:
1. Se realizan las operaciones que están dentro de los paréntesis. Si hay unos dentro de otros, se empieza por los internos.
2. Se efectúan las multiplicaciones y divisiones de izquierda a derecha.
3. Se realizan las adiciones y sustracciones de izquierda a derecha.
NOTA:
1. Desarrollar ejercicios con operaciones combinadas de números enteros.
2. Practicar la solución de problemas que involucren operaciones combinadas con números enteros.
ACTIVIDADES PRACTICAS:
Juegos de ingenio matemático que ayuden a desarrollar el pensamiento lógico y predispongan al grupo para la comprensión del nuevo tema.
MARCO TEÓRICO:
Operaciones sin paréntesis:
Para resolver operaciones combinadas con números enteros, se les da prioridad a algunas operaciones con respecto a otras; es decir, existe una jerarquía de las operaciones que indica el orden en que estas deben ser efectuadas. En este caso, el orden correcto en el que se debe resolver la operación presentada es: primero se realiza la división y luego la adición.
1. Se resuelven las multiplicaciones y divisiones de izquierda a derecha.
2. Se resuelven las adiciones y sustracciones de izquierda a derecha.
Operaciones con paréntesis
Cuando hay operaciones combinadas en las que aparecen signos de agrupación, el orden para resolverlas es el siguiente:
1. Se realizan las operaciones que están dentro de los paréntesis. Si hay unos dentro de otros, se empieza por los internos.
2. Se efectúan las multiplicaciones y divisiones de izquierda a derecha.
3. Se realizan las adiciones y sustracciones de izquierda a derecha.
NOTA:
Cuando delante de un paréntesis hay un signo menos, el paréntesis se puede eliminar de dos maneras, sin alterar el resultado de la operación contenida en él.
• Se efectúan primero las operaciones contenidas en el paréntesis y se halla el opuesto del resultado.
• Se aplica la propiedad distributiva de la multiplicación con respecto a la adición y se cambia el signo de los sumandos.
DESARROLLO DE COMPETENCIAS:
1. Desarrollar ejercicios con operaciones combinadas de números enteros.
2. Practicar la solución de problemas que involucren operaciones combinadas con números enteros.
ACTIVIDADES PRACTICAS:
- Efectúa la operación -3 - (-7 + 12) de dos formas distintas
TRABAJO EXTRA CLASE:
FECHA: 21/02/2020
ACTIVIDAD N° 2
TEMA: Igualdades, ecuaciones e inecuaciones en Z
OBJETIVO: Propone y ejecuta procedimientos para resolver
una ecuación lineal y sistemas de ecuaciones
lineales y argumenta la validez o no de un
procedimiento.
ACTIVIDAD INICIAL:
MARCO TEÓRICO:
Igualdades
Una igualdad es una relación entre dos expresiones matemáticas que representan el mismo valor. Las igualdades tienen dos miembros separados por el signo igual (=).
Una igualdad actúa como una balanza en equilibrio, como se sugiere en la Figura
Ejemplo
Los siguientes son ejemplos de igualdades matemáticas. En todos se obtiene 16 utilizando diferentes operaciones.
8 x 2 = 16 5 + 5 + 6 = 16 32 / 2 = 16
Propiedades de las igualdades
Si a, b y c son números naturales cualesquiera, tales que a = b, entonces se satisfacen las siguientes igualdades:
La primera propiedad menciona que al adicionar o sustraer la misma cantidad en ambos miembros de una igualdad, la igualdad se conserva. La segunda propiedad indica que al multiplicar o dividir ambos miembros de una igualdad por la misma cantidad (diferente de cero), la igualdad se conserva.
Ecuaciones
Una ecuación es una igualdad en la cual hay términos conocidos y términos desconocidos. El término desconocido se llama incógnita y se representa generalmente por letras minúsculas del abecedario.
La ecuación se resuelve cuando se encuentra el valor o los valores de la o las incógnitas que hacen verdadera la igualdad. Este valor recibe el nombre de solución.
Ejemplo
La igualdad x + 25 = 36 es una ecuación porque uno de sus términos es desconocido. La incógnita en este caso está representada por la letra x. Al reemplazar la incógnita por 11 se verifica la igualdad
11 + 25 = 36, lo que significa que x = 11 es la solución de la ecuación.
Ejemplo
Para que 2 x m + 5 = 21, m debe reemplazarse por 8, ya que: 2 x 8 + 5 = 21. Cualquier otro valor de m hace que no se conserve la igualdad. Por ejemplo, si m = 1, se tiene que 2 x 1 + 5 no es igual a 21.
Ecuaciones aditivas y multiplicativas
Inecuaciones
Una desigualdad es una expresión que compara dos cantidades que no son iguales. Así como la igualdad se representa mediante una balanza en equilibrio, una desigualdad se representa como una balanza inclinada hacia alguno de los lados. Una desigualdad que contiene al menos una variable se denomina inecuación.
MARCO TEÓRICO:
Igualdades
Una igualdad es una relación entre dos expresiones matemáticas que representan el mismo valor. Las igualdades tienen dos miembros separados por el signo igual (=).
Una igualdad actúa como una balanza en equilibrio, como se sugiere en la Figura
Ejemplo
Los siguientes son ejemplos de igualdades matemáticas. En todos se obtiene 16 utilizando diferentes operaciones.
8 x 2 = 16 5 + 5 + 6 = 16 32 / 2 = 16
Propiedades de las igualdades
Si a, b y c son números naturales cualesquiera, tales que a = b, entonces se satisfacen las siguientes igualdades:
La primera propiedad menciona que al adicionar o sustraer la misma cantidad en ambos miembros de una igualdad, la igualdad se conserva. La segunda propiedad indica que al multiplicar o dividir ambos miembros de una igualdad por la misma cantidad (diferente de cero), la igualdad se conserva.
Ecuaciones
Una ecuación es una igualdad en la cual hay términos conocidos y términos desconocidos. El término desconocido se llama incógnita y se representa generalmente por letras minúsculas del abecedario.
La ecuación se resuelve cuando se encuentra el valor o los valores de la o las incógnitas que hacen verdadera la igualdad. Este valor recibe el nombre de solución.
La igualdad x + 25 = 36 es una ecuación porque uno de sus términos es desconocido. La incógnita en este caso está representada por la letra x. Al reemplazar la incógnita por 11 se verifica la igualdad
11 + 25 = 36, lo que significa que x = 11 es la solución de la ecuación.
Ejemplo
Para que 2 x m + 5 = 21, m debe reemplazarse por 8, ya que: 2 x 8 + 5 = 21. Cualquier otro valor de m hace que no se conserve la igualdad. Por ejemplo, si m = 1, se tiene que 2 x 1 + 5 no es igual a 21.
Ecuaciones aditivas y multiplicativas
Inecuaciones
Una desigualdad es una expresión que compara dos cantidades que no son iguales. Así como la igualdad se representa mediante una balanza en equilibrio, una desigualdad se representa como una balanza inclinada hacia alguno de los lados. Una desigualdad que contiene al menos una variable se denomina inecuación.
ACTIVIDAD N° 1
TEMA: Repaso de números enteros
OBJETIVO: Reforzar el concepto y manejo de las operaciones con números enteros, a través de ejercicios en clase.
ACTIVIDAD INICIAL:
hacer una actividad lúdica con los estudiantes que ayude a mejorar el desarrollo del pensamiento matemático.
MARCO TEÓRICO.
NÚMEROS ENTEROS
El conjunto de los números enteros:
En ocasiones no es suficiente el conjunto de los números naturales para representar matemáticamente situaciones de la vida cotidiana. Por esta razón, los matemáticos de la antigüedad consideraron necesario ampliar este conjunto y comenzar a utilizar los números negativos.
Esta decisión dio origen al conjunto de los números enteros (Z), el cual incluye los enteros negativos (Z-), los enteros positivos (Z+) y el 0.
En ocasiones no es suficiente el conjunto de los números naturales para representar matemáticamente situaciones de la vida cotidiana. Por esta razón, los matemáticos de la antigüedad consideraron necesario ampliar este conjunto y comenzar a utilizar los números negativos.
Esta decisión dio origen al conjunto de los números enteros (Z), el cual incluye los enteros negativos (Z-), los enteros positivos (Z+) y el 0.
DESARROLLO DE COMPETENCIAS:
TRABAJO EXTRA CLASE: