07 de Noviembre 2020 (No tienen jornada académica)
24 de Octubre 2020
- Explicación teorema del coseno, por medio de ejemplos.(Videos adjuntos vía WhatsApp)
- Actividad Adjunta
03 de Octubre 2020
- Explicación teorema del coseno, por medio de ejemplos.(Videos adjuntos vía WhatsApp)
- Actividad Adjunta
19 de septiembre 2020
05 de septiembre 2020
Actividad
15 de Agosto 2020
El docente envía vídeos al grupo de whatsap, dando las explicaciones.
ACTIVIDAD
01 de Agosto 2020
Para complementar la información, ver el siguiente vídeo:
El docente enviara un vídeo.
Resolver:
Julio
18/2020
Ángulos en posición normal, medición de ángulos en
el sistema sexagesimal, ángulos coteminales
Ver el siguiente vídeo: https://www.youtube.com/watch?v=j5pjx7mjmwE
Actividad
Resolver hasta el punto 20.
Semestre 2
JUNIO 13 DE 2020
Concepto de porcentaje
La palabra porcentaje procede del vocablo inglés "percentyage" pero surgió de la unión de los siguientes términos tomados de la lengua latina: el prefijo "por" que alude en este caso a la acción de multiplicar; "centum" que hace referencia al número "cien" y el sufijo de globalidad "aticum".
Ámbitos de uso
En matemática, se denomina porcentaje, o tanto por ciento, a una porción proporcional del número 100, por lo tanto puede expresarse como fracción. Si decimos 50 % (este es el símbolo que representa el porcentaje) significa la mitad de cien; el 100 % es el total. Si decimos que el 15 % de la ciudad trabaja de modo informal, son 15 de cada 100 que lo hacen de ese modo, mientras, que, el 85 %, por exclusión, tendría acceso al mercado formal, siempre que se haya tomado para el estudio, exclusivamente, a toda la población económicamente activa.
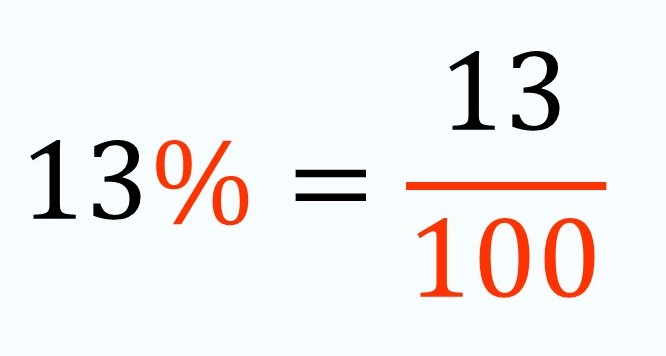
- Taller
MAYO 29 DE 2020
¿Qué es la regla de 3 simple?
La regla de 3 simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa.
Para hacer una regla de tres simple necesitamos 3 datos: dos magnitudes proporcionales entre sí, y una tercera magnitud. A partir de estos, averiguaremos el cuarto término de la proporcionalidad.
Regla de 3 simple directa
Empezaremos viendo cómo aplicarla en casos de proporcionalidad directa (cuando aumenta una magnitud también lo hace la otra).
Colocaremos en una tabla los 3 datos (a los que llamamos «a», «b» y «c») y la incógnita, es decir, el dato que queremos averiguar (que llamaremos “x”). Después, aplicaremos la siguiente fórmula:
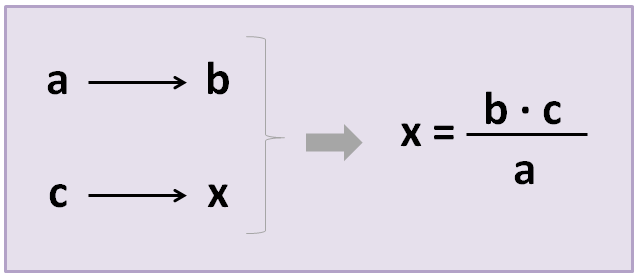
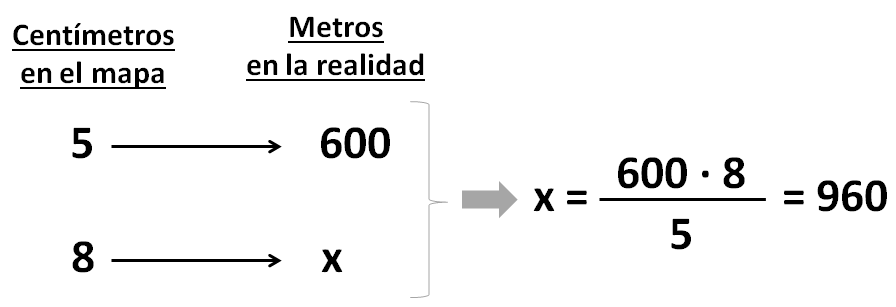
Ejemplo: Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos han dicho que 5 centímetros del mapa representan 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?

Regla de 3 simple inversa
Ahora vamos a ver cómo aplicar la regla de 3 simple en casos de proporcionalidad inversa (cuando aumenta una magnitud disminuye la otra).
Colocaremos los 3 datos y la incógnita en la tabla igual que los hemos colocado en el caso anterior. Pero aplicaremos una fórmula distinta:
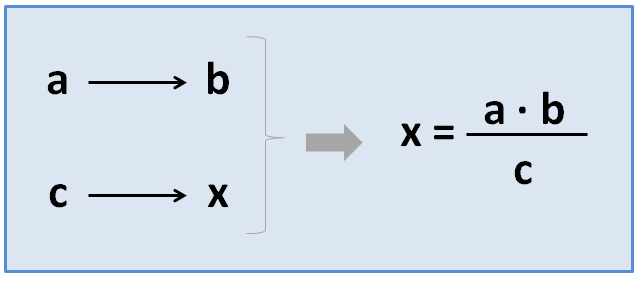

Ejemplo :Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?
Colocamos los datos en una tabla y aplicamos la fórmula de la regla de 3 simple inversa:
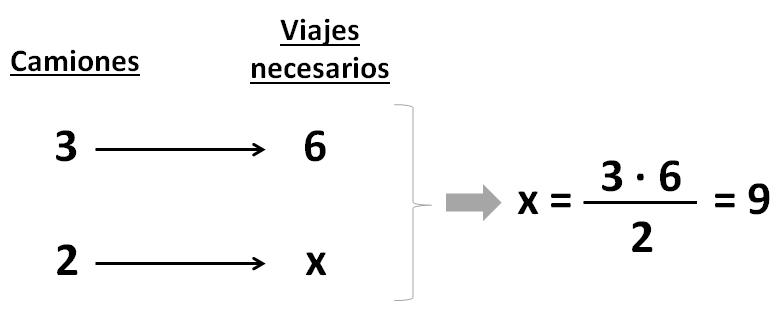
Solución: Ayer los 2 camiones hicieron 9 viajes.
https://www.youtube.com/watch?v=OyEcoAV3oFY Identificar las relaciones
https://www.youtube.com/watch?v=uQO_oBKqypQ Regla de 3 simple directa
https://www.youtube.com/watch?v=OyEcoAV3oFY Identificar las relaciones
https://www.youtube.com/watch?v=uQO_oBKqypQ Regla de 3 simple directa
MAYO 15 DE 2020
IDENTIDADES TRIGONOMÉTRICAS
Una identidad trigonométrica es una igualdad entre expresiones que involucran funciones trigonométricas y que es verdadera para todos los valores de la variable (o ángulo) en los que están definidas. A partir del teorema de Pitágoras podemos derivar las identidades fundamentales o básicas y a partir de éstas otras, generalmente denominadas auxiliares.

Actividades
1. Escribir la definición anterior y sus ejemplos
2. ver video https://www.youtube.com/watch?v=CRg5jQRj1Hg
3. Resolver los ejercicios propuestos por el docente y enviar evidencia digital.
Una identidad trigonométrica es una igualdad entre expresiones que involucran funciones trigonométricas y que es verdadera para todos los valores de la variable (o ángulo) en los que están definidas. A partir del teorema de Pitágoras podemos derivar las identidades fundamentales o básicas y a partir de éstas otras, generalmente denominadas auxiliares.

Actividades
1. Escribir la definición anterior y sus ejemplos
2. ver video https://www.youtube.com/watch?v=CRg5jQRj1Hg
3. Resolver los ejercicios propuestos por el docente y enviar evidencia digital.
1. Escribir la definición anterior y sus ejemplos
2. ver video https://www.youtube.com/watch?v=CRg5jQRj1Hg
3. Resolver los ejercicios propuestos por el docente y enviar evidencia digital.
MAYO 01 DE 2020
Relaciones trigonométricas
Las relaciones trigonométricas son igualdades entre expresiones matemáticas que contienen funciones trigonométricas y son aplicables a todos los valores del ángulo en los que se encuentren definidas las funciones, así como cualquier operación aritmética involucrada. Algunas de las relaciones usadas en las relaciones trigonométricas provienen del Teorema de Pitágoras.
Relaciones trigonométricas fundamentales
Las relaciones trigonométricas son ecuaciones que contienen funciones trigonométricas y que a su vez son equivalentes para todos y cada uno de los valores de las variables involucradas. Las razones trigonométricas constituyen la base de los ejercicios de trigonometría que podemos desarrollar en matemáticas.
Las relaciones trigonométricas se utilizan para la simplificación de expresiones trigonométricas, es decir, que son útiles para mostrar que cada vez que se cumple la primera expresión matemática, se cumplirá la segunda expresión. Dichas relaciones se dividen en tres categorías distintas, cocientes, pitagóricas y recíprocas, se conocen como:
Cómo pasar de radianes a grados paso a paso
Para pasar de radianes a grados, lo hacemos igual que antes, con una regla de 3, solo que esta vez, la incógnita a despejar serán los grados.Vamos a verlo con un ejemplo:¿Cuántos grados son 3π /4 radianes? Planteamos la regla de tres: Si π radianes son 180º, 3π/4 radianes serán x grados:

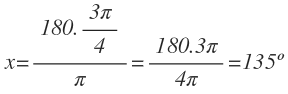
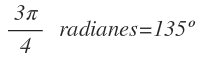
Evaluación trigonométria
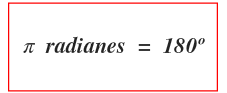




FEBRERO 08 DE 2020
FEBRERO 15 DE 2020
Qué son los radianes
Para medir los ángulos se pueden utilizar dos unidades: los grados sexagesimales y los radianes. Ambas unidades son equivalentes
¿Y qué significa que sean equivalentes?
Pues que para el mismo ángulo, su valor lo puedes dar en ángulos o en radianes y por tanto se puede convertir de una unidad a otra.
Normalmente, estamos más familiarizados con los grados, ya que es lo primer que nos enseñan. Como ya sabes, una vuelta completa de circunferencia tiene 360º:
Equivalente entre grados y radianes
La equivalencia entre grados y radianes es la siguiente:
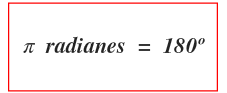
Cómo pasar de grados a radianes paso a paso
Para pasar de grados a radianes lo hacemos mediante una regla de tres, teniendo en cuenta la equivalencia entre radianes y grados.
Por ejemplo, ¿cuántos radianes son 60º?
Planteamos la regla de tres: Si 180º son π radianes, 60º serán x radianes. Ponemos los grados debajo de los grados y los radianes debajo de los radianes:

Y ahora despejamos la x:

Ya sólo nos queda operar. Para dejarlo el resultado en múltiplos de π , simplificamos los números que tenemos en la operación y nos queda:

Ver vídeo:
FEBRERO 08 DE 2020
¿Qué es la trigonometría?
La trigonometría es la rama de las matemáticas que estudia la relación entre los lados y ángulos de los triángulos. Se ocupa, por tanto, de las funciones asociadas a los ángulos, denominadas funciones trigonométricas (también pueden denominarse funciones circulares): seno, coseno, tangente, secante,…Etimológicamente, trigonometría significa medida de los triángulos, ya que proviene de las palabras griegas trígono (triángulo) y metría (medida).
¿Qué es el sistema sexagesimal?
El Sistema sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de los ángulos.
Tiempo
1 h ----- 60 min
1 min ----- 60 s
Grados sexagesimales
1º ----- 60'
1' ----- 60''
Tiempo
1 h ----- 60 min
1 min ----- 60 s
Grados sexagesimales
1º ----- 60'
1' ----- 60''


























